Casamm2 para m2

Computing Enclosures for the Matrix Mittag–Leffler Function

Por um escritor misterioso
Last updated 10 novembro 2024
Computing Enclosures for the Matrix Mittag–Leffler Function
Computing Enclosures for the Matrix Mittag–Leffler Function
A Rational Approximation Scheme for Computing Mittag-Leffler Function with Discrete Elliptic Operator as Input
Computing Enclosures for the Matrix Mittag–Leffler Function
The case, arg z, < πα In this case, if 0 < < <, z, , then z is in the
Computing Enclosures for the Matrix Mittag–Leffler Function
PDF] Differentiation of the Mittag-Leffler Functions with Respect to Parameters in the Laplace Transform Approach
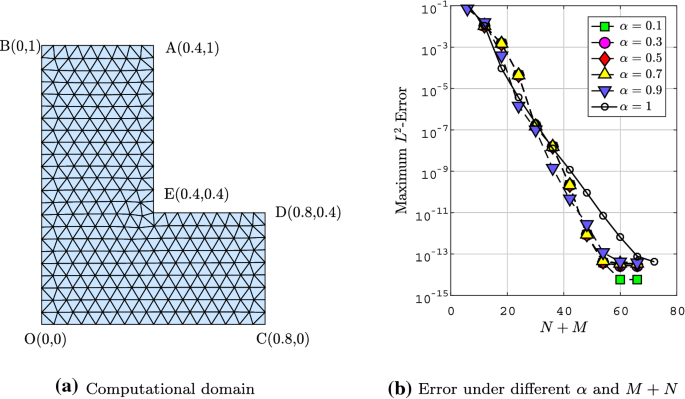
Computing Enclosures for the Matrix Mittag–Leffler Function
A Rational Approximation Scheme for Computing Mittag-Leffler Function with Discrete Elliptic Operator as Input
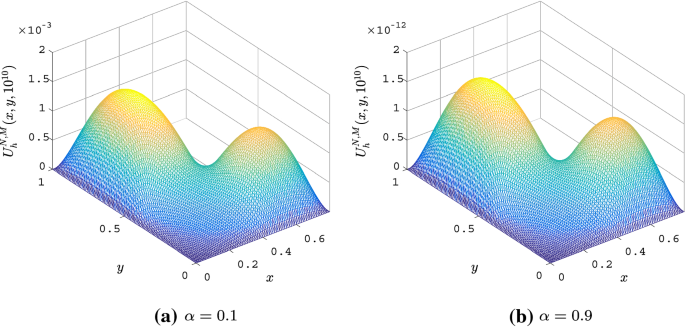
Computing Enclosures for the Matrix Mittag–Leffler Function
Fractal Fract, Free Full-Text
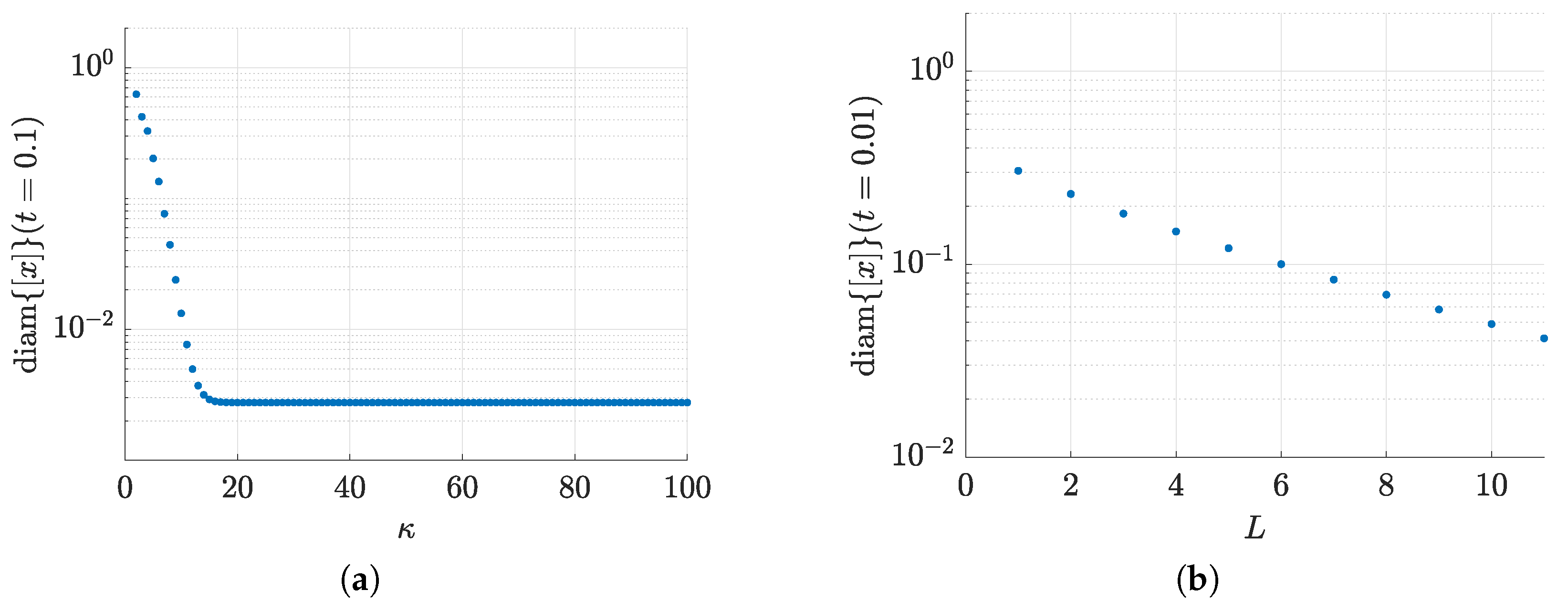
Computing Enclosures for the Matrix Mittag–Leffler Function
A Rational Approximation Scheme for Computing Mittag-Leffler Function with Discrete Elliptic Operator as Input
Computing Enclosures for the Matrix Mittag–Leffler Function
PDF) Computing the Matrix Mittag-Leffler Function with Applications to Fractional Calculus
Computing Enclosures for the Matrix Mittag–Leffler Function
The function E α,β (−t) for α = 0.25, β = 1 and its derivative. Black
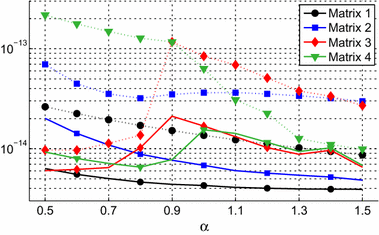
Computing Enclosures for the Matrix Mittag–Leffler Function
Computing the Matrix Mittag-Leffler Function with Applications to Fractional Calculus
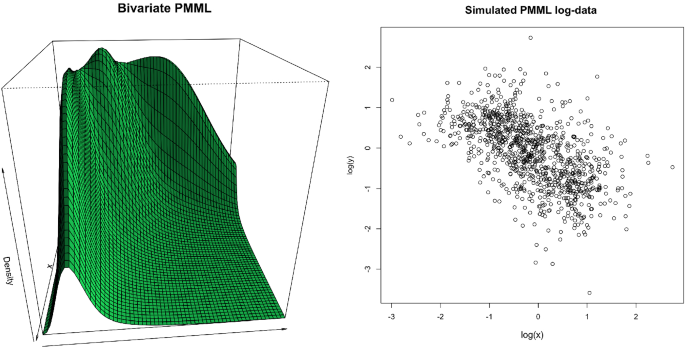
Computing Enclosures for the Matrix Mittag–Leffler Function
Multivariate matrix Mittag–Leffler distributions Annals of the Institute of Statistical Mathematics
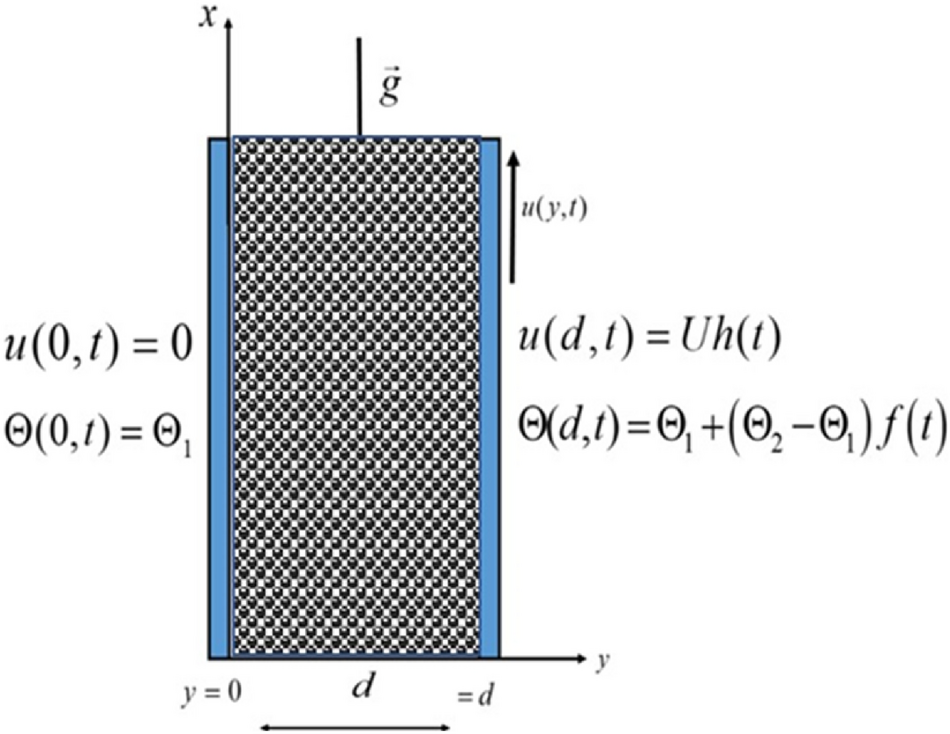
Computing Enclosures for the Matrix Mittag–Leffler Function
Enhancement in heat transfer due to hybrid nanoparticles in MHD flow of Brinkman-type fluids using Caputo fractional derivatives
Computing Enclosures for the Matrix Mittag–Leffler Function
The function E α,β (−t) for α = 0.25, β = 1 and its derivative. Black
Recomendado para você
você pode gostar

© 2014-2024 lexenimomnia.com. All rights reserved.